Deep dive into Lamport clock and Lamport Vector clock.

This blog is in continuation of the previous blog. In the previous blog, we had discussed the types of ordering and the types of events that happen on a distributed system. We got familiar with the concept of causality. When we say the concept of causality we mean those three rules that help us determine the causality between the events and If events don't comply with the causality relation we consider them as concurrent events.

If all the paragraph above did not make sense to you, I highly recommend you to read this blog before continuing.

As promised, today we are going to discuss two concepts.

• How the concept of causality is a potential casualty.

• How Lamport clocks help us to determine causality between different events.

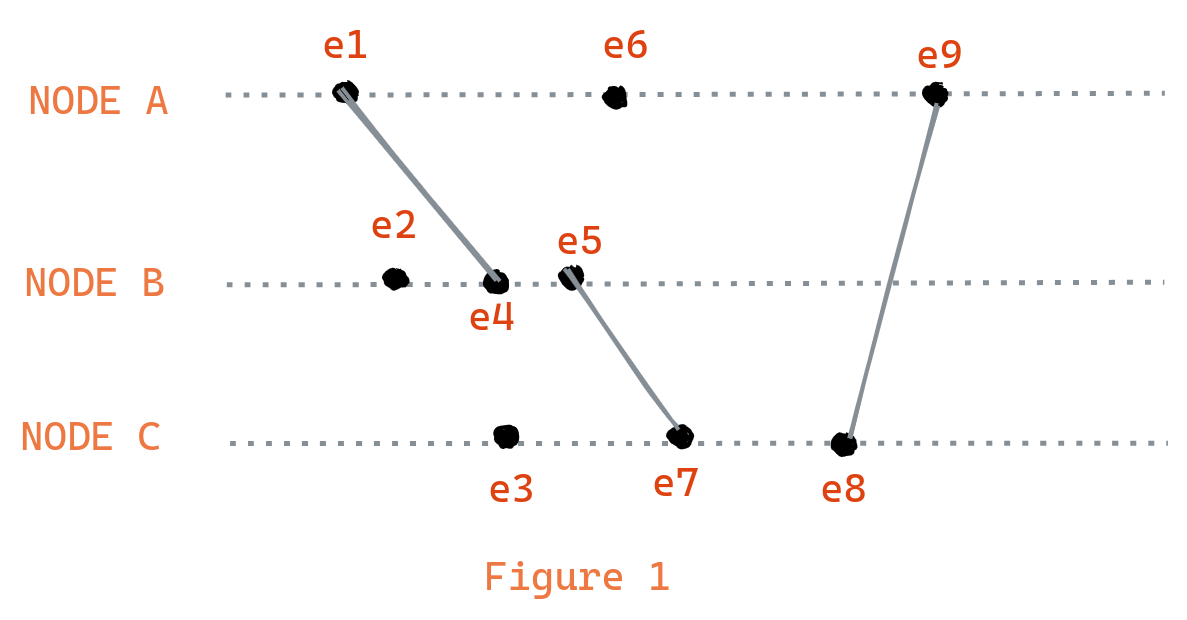
The concept of causality

If we apply the concept of causality rules in the above diagram of events. We can infer the following relationships: e₁ -> e₄ , e₁ -> e₅, e₁ -> e₆, e₁ -> e₉, e₁ -> e₇ and e₁ -> e₈. However, note that e₁ || e₃ and e₂ || e₆ even after occurring at a distant time because we don't have enough information to track the causality relation between them. This is means that events are considered concurrent by the system because they could have happened in any order as there were no information exchanged between them.

This is the reason why the concept of causality is referred to as potential causality. Lamport clock are a logical clock that were invented to solve this problem.

Lamport clocks

Lamport clocks are a logical clock and numeric in nature. In a distributed system, each node maintains their lamport clocks and starts it from zero when the nodes start operating.

To increment the value of a logical clock when executing an event, each node has to follow the following protocols.

• Before executing an event (send, receive or local) the node increments the counter of its logical clock. LC = LC + 1

• Every message sent across the distributed system piggybacks the counter value of its sender at the sending time. The node which receives the message executes the following command. - Updates its clock with the maximum of its clock value and the sender's clock value. - Executes the message at its end. - Delivers the message.

To understand how Lamport clocks work let take a look at the example above, here we have a distributed system consisting of three nodes (A, B and C). If we observe all the event are abiding the protocols of incrementing their clocks while performing events.

Let's pick any two events that are causaly related, A₁ and B₁ are causally related (A₁ -> B₁). We can observe that if one event causally preceds other then C(A₁) < C(B₁).

However, we need to observe that the oppposite is not true. If two event exists such that C(e₁) < C(e₂), it does not necessarily means that e₁ causally preceds other. For example, Take a look at C₂ and B₂ in the diagram. C(C₂) < C(B₂) but C₂ and B₂ are not causally related , B₂ could have happened before C₂ with the same clock value.

Hence, Lamport clocks satisfy so-called clock consistency condition: If one event e₁ causally precedes other event e₂ then C(e₁) < C(e₂). But it does not satify the strong consistency condition: If C(e₁) < C(e₂) then e₁ causally precedes e₂.

Lamport Vector Clocks

As we realised that Lamport clocks are not good enough to determine the causal relationship between the events because they fail the strong consistency condition. The reason behind this is that in Lamport clocks we are trying to flat the global and local clocks together. As a result, events don't know about all the events that precede it.

A set of all the events that causally precedes an event is known as Causal History.

For instance, In the figure above the causal history of e₇ is {e₁,e₂,e₃,e₄,e₅}.

We have to solve this problem cost-effectively and utilizing a compact data structure. A Vector clock is an example of such a data structure.

A vector clock is another type of logical clock, where the clock data stucture of each node is an array of N counters (where N is the number of nodes present on the distributed system) [c₁, c₂, c₃, c₄, ... ,c_N].

• The i^th element of the vector represent the local logical clock for that node.

• The remaining element represents the global logical clock of the nodes. [c₀, c₁, ..., c_i-1, c_i+1 , ..., c_n-1, c_N].

Just like Lamport clocks, there are protocols for each node to follow to update their logical clock:

• Before executing an event (receive, send or local) increment the counter of its logical clock. c_i = c_i + 1.

• Every message sent acorss the distributed system piggybacks the counter vector of its sender at the sending time. When the i^th node receives the j^th node counter vector [c_j0, c_j1, c_j2, c_ji, ... ,c_jN]. - Executes the received message. - Updates each index of the its vector clocks by taking the maximum of the corresponding index from the j^th vector clock. C_i,k = max(C_i,k,C_j,k). - Delievers the message.

This kind of logical clock satisify the strong consistency condition. That means if two events e₁ and e₂ exists with timestamp of C₁ and C₂, such that C(C₁) < C(C₂) then e₁ causally precedes e₂ (e₁ -> e₂).

The only thing missing is to discuss how to compare Lamport vector clocks with each other, which is done in the following way.

• For 2 vector clocks C_i = [C_i,0, ..., C_i,N] and C_j = [C_j,0, ..., C_j,N], C_i < C_j iff all the elements of clock C_i is less than the corresponding elements from clock C_j (C_i,k ≤ C_j,k for all k) and there exist a single element in C_i that is strictly less than the corresponding element in C_j. (C_i,L<C_j,L for atleast one L in [1...N])

In the figure above, we can observe that the clocks are updated following the protocaols describe above. This time we can say that C(A₁) <C(B₁) while A₁-> B₁. What is most important is that we can determine if two events are causally related or concurrent. B₂ || C₂ since C(B₂) is neither less than or greater than the C(C₂).

Vector clocks are useful for a situation that benefits from determining whether two events are causally related or concurrent. That too allowing the nodes to progress independently without any bottlenecks of synchronization or coordination.

However, there exists a possible problem with vector clocks. Each node has to maintain a vector of N length. N is the number of nodes contributing to the distributed system. In our examples, our N is fairly low but in real-life scenarios, this could grow in an exponential and unmanageable number. For example, if a distributed system of an application considers every browser as a node.

Let's take a break. In the next blog, we will discuss partitioning in distributed systems and its types.

See you 👋